Van Schooten's Elliptic Orbit Machine
Click the triangular "play" button in the lower left to animate the diagram (and turn off "Show image.")
If you can't drag the points, try double-clicking in the geometry window to open a separate window.
This figure is taken from a popular seventeenth century text by Franz van Schooten, originally published in 1657 entitled: Organica Coniccarum Sectionum in Plano Descriptione (Organs for the Description of Conic Sections in the Plane). Van Schooten was a Dutch friend of Descartes
who published an edition of Descartes' Geometry with extensive commentaries. Van Schooten's edition of Descartes was much more popular than the original and was one of the first mathematical works read by Newton, along with this work of conic sections.
Questions to think about
One definition of an ellipse is the set of points equidistant from a circle (directrix) and a point inside the circle (focus). This is analogous to the focus/directrix definition of a parabola, where the directrix is a line.
- Why and how does this diagram use the focus/directrix definition of an ellipse?
- Try starting with this construction and obtaining another of the ways to define an ellipse:
- Given two points, F1 and F2 (foci) and a fixed length, an ellipse is the set of points the sum of whose distances from F1 and F2 is the fixed length. (The string and tacks definition)
- The set of points satisfying an equation of the form
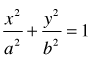 in some coordinate system. in some coordinate system.
- A circle that has been stretched in one direction.
- The shadow of a circle.
- A cross section of a cone by a plane that intersects only one nappe of the cone (and is not parallel to a tangent plane of the cone.)
Susan Addington, Created with GeoGebra |

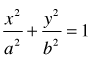 in some coordinate system.
in some coordinate system.