Mathematical Intentions

A Complete Ethnomathematical History of Our Current Secondary Mathematics Curriculum.

This website contains fifty half-hour lectures by David Dennis, in mp3 format, many supporting documents in PDF format, and interactive applets by Susan Addington in dynamic geometry and spreadsheets.

The webiste takes apart every major idea in our current mandatory secondary mathematics curriculum (Algebra I--AP Calculus) and asks three historical questions.

What were the scientific, social, religious, political and economic intentions of the people who created this mathematics?
When and why were these mathematical ideas made into mandatory curriculum? And what parts of the original mathematics have we dropped from our curriculum?
Why do we still teach this curriculum? And how will it be transformed by new technology?

Thus for every mathematical idea taught in high school, these three different intentions will be described. Seemingly epic in scope, this task is easier than one might, at first, suspect, since much of our mandatory mathematics curriculum comes from a rather narrow piece of social history. For example, the English Civil Wars of the 17th Century and their aftermath yield a huge ammount of our current notions of school mathematics, and so the social history of the Puritan movement must be examined in detail, along with the Jesuit response. Once we understand their intentions we can ask much deeper questions about what pieces of their curriculum we still want to require of our students. Do we still believe that the natural world is “God's other book?” Do we continue to accept the radical pragmatisim and religious pluralism that led to Oliver Cromwell’s “new model army?”

Intentions matter! Especially when mandatory curriculum is tied to high stakes testing. This site is intended to get all of the relevant historical cards on the table as quickly and as effciently as possible, specifically to aid in the reform of mathematics curriculum. Surprising answers are given to nagging questions that are glossed over in secondary curriculum, like “Where did fractional exponents come from? And what are they good for?” What was the role of tables, and how does that change with modern spreadsheets? Many historical examples are shown embedded in new transtormational computer environments, e.g. animations of Descartes’ curve drawing machines.

This website is a large scale attempt to carry out the research program described in:

Dennis, D. (2000). The Role of Historical Studies in Mathematics and Science Educational Research. In Dick Lesh & Anthony Kelly (Eds.) Handbook for Research Design in Mathematics and Science Education. Mahwah, NJ: Lawrence Erlbaum.

In that chapter I described three increasing levels of impact that history can have on curriculum development: Context, Content, and Critique. This website engages all three levels for every secondary mathematical topic, in the hope that the fruits of historical understanding, in a convienient form, can nourish the technological transformation of school mathematics.

How to use these materials

The lectures give a survey of the mathematics, as well as its social-historical background. They are the main framework for the whole project.

Most lecture notes have associated applets: small interactive programs to illustrate a mathematical concept. When the lecture notes include a picture, the applet gives infinitely many variations on the picture, or sometimes a picture in motion.

Most lectures that describe mathematics have corresponding lecture notes. These supplement the lectures with details of the mathematics, and include exercises, some mandatory, and some for further exploration. Sometimes several lectures discuss the mathematics in one lecture notes document, and vice versa. The lectures discuss the topics in approximate historical order, with occasional departures for mathematical historical background.

Note: This website was put up during 2010, but more applets and lecture notes appear periodically. Please check back for additional material.

We welcome your comments. Send them to david.dennis@earthlink.net.

Podcasts

Lecture	Lecture notes	Applets
Click to open a window to play the podcast. The audio player should open in a separate tab or window.	PDF files to read with the lecture. These include links to the applets. There are exercises and problems for the serious reader to do. Right-click or control-click to download instead of of opening.	Interactive demonstrations, mostly on GeoGebraTube. Some are spreadsheets, mostly on Google Docs. There are also links to applets made by others. [We're moving the applets to the GeoGebra website in 2018. In the meantime, some don't work. Please check back later. Ones that do are marked with a *. ] Right-click or control-click to download or open in a new window.
1. How Did We Get Here?
2. Puritan Printheads
3. The Firing Line
4. A Car is not a Horseless Carriage
5. Observable Units
6. Corporations and Kinship
7. Puritans and Race in America
	Navigating GeoGebra (how to run the applets)
	Geometric Constructions
	Similarity, Geometric Arithmetic, and the Geometric Mean	Similar Triangles * Similar Quadrilaterals * Similar Pentagons * Triangles Inscribed in a Circle * Three Similar Right Triangles * The Geometric Mean * Square Root Construction *
8. Slide Rules and Logarithms 9. A Discourse on Method 10. Square Roots and Logarithms 11. Linkages and Logarithms	Square Roots Graph paper in inches and tenths Napier Rods Slide Rules and Logarithm Tables Napier's Mirifici Logarithmorum Canonis Descriptio (1614) PaperSlideRule Descartes's Logarithm Construction	Babylon Square Root Algorithm * Hindu Square Root Algorithm * European Square Root Algorithm * Making a Logarithm Table * Virtual Slide Rule, by Derek Ross * Descartes's Logarithm Machine * Descartes's Two Mean Proportionals Machine Descartes's Logarithm Graph Slope of the Logarithm Graph
12. Geometry Fades Away
13. Flattening Apollonius	Apollonius and Conic Sections (information with problems) Parabolas and Coordinates (problems/activities)	Some of these 3D applets need the Cabri3D plugin (free; Mac and Windows only). We're updating to GeoGebra. Cone from a Rotating Line * Symmetry of an Oblique Cone Tangent Plane to a Cone Circular Sections of a Cone Conic Sections Conic Sections: Parabola 1 Conic Sections: Parabola 2 Conjugate Diameters of an Ellipse Conjugate Diameters of a Parabola
14. Parabolas and Tangents	Functions of a Curve: Leibniz's Original Notion of Functions and its Meaning for the Parabola (paper by Dennis and Confrey) Ellipses (problems/activities)	Parabola constructed by a Rhombus Parabola by Focus and Directix Quadrivium Logo Ellipse Construction Van Schooten's Elliptic Orbit Machine
15. Hyperbolas and Ratios	Descartes's Hyperbola Construction
16. Refraction and Efficiency
17. Pascal and Nature
18. Pascal's Triangle and Induction	"A Treatise on the Arithmetical Triangle" (Translation of Pascal's paper, with an investigation/project written by David Pengelley)	Adjustable Pascal's Triangle *
19. Summation and Difference
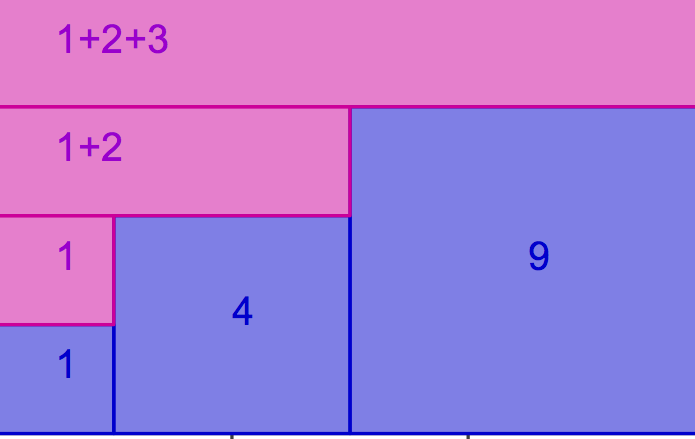20. The Summations of Ibn-al-Haitham	Al Hazen's Summation Formulas	AlHazen1 The Sum of Integers: 1+2+3+... * AlHazen2 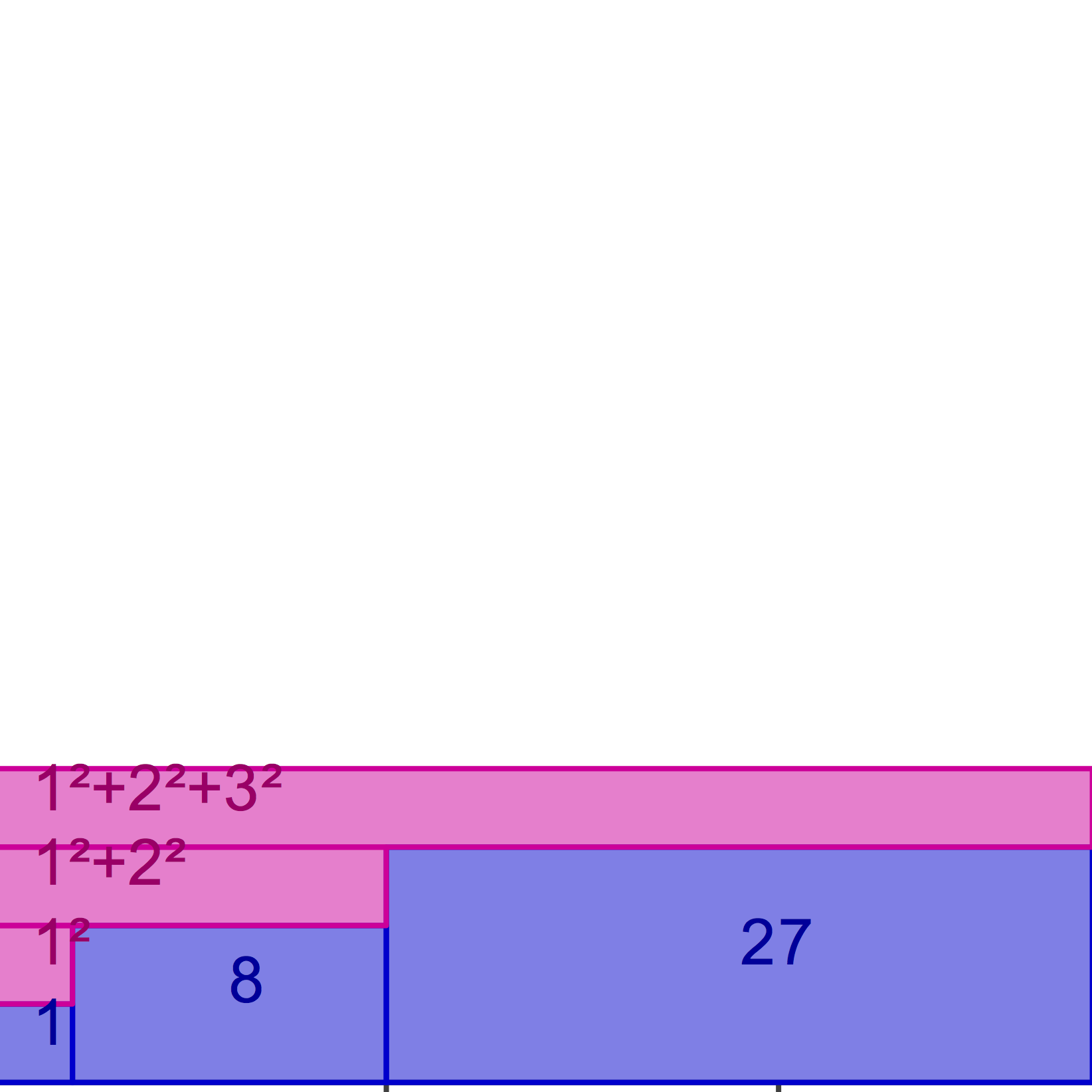The Sum of Squares: 1²+2²+3²+... AlHazen3 The Sum of Cubes: 1³+2³+3³+... ParabDome
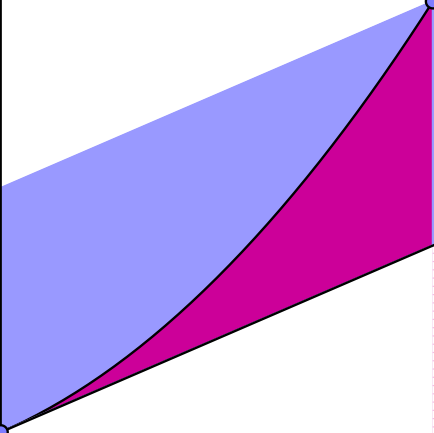21. Characteristic Ratios	Newton and Characteristic Ratios	ParabArea 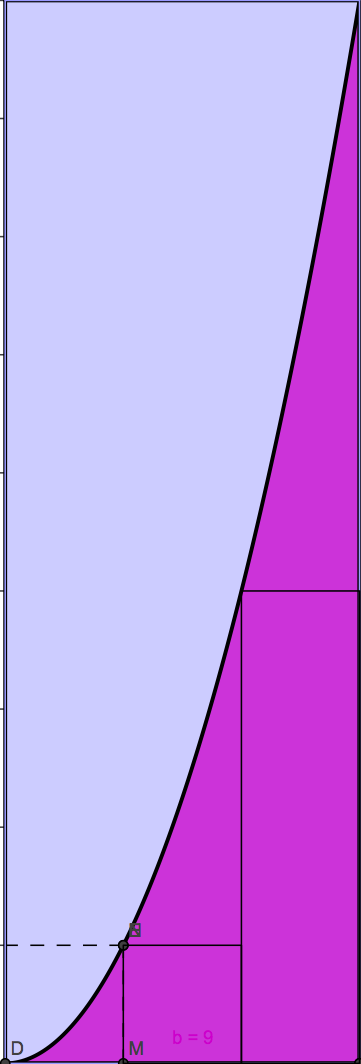CharRatioXtoN
22. Wallis and Cromwell
23. Reading, Writing, and Arithmetic
24. Wallis and Fractional Exponents 25. Wallis and Pi 26. The Impact of Wallis 27. Newton Reads Wallis 28. Newton's Binomial Series 29. Interpolation and Continuity 30. Experiments with Technology	Wallis and Fractional Exponents Wallis and Negative Exponents Newton's Binomial Series Euler and the Exponential Base e NewtonInterpolation	WallisTable * WallisNewtonTable *
31. Purity and Abstraction
32. Culture, Motion, and Language
33. The Challenge of the Cycloid	The Cycloid: Tangents, Velocity Vector, Area, and Arclength	CycloidArea CycloidTangent
34. Trigonometry		TrigSegments
35. Leibniz and Transmutation	Transmutation	[In progress. Please read the Lecture Notes for explanations.] Transmutation_Lin PascalIntSin TransmuteCircle TransmuteConics
36. Testing the Leibniz Rules
37. The Textbooks of Euler		See the complex number applets with Lecture 45
38. The Children of Euler
39. Weierstrass and Godel
40. The Quest for Certainty
41. The Shape of Averages
42. Personality and Structure
43. God's Other Book
44. Mathematics and Art
45. The Future of Curriculum		Complex Addition * Complex Multiplication * Complex Reciprocal * Complex Squaring Function * Complex Square Root Function * Complex Exponential Function * Complex Logarithm Function * Complex Sine Function *
46. Does Algebra Teach You to Think?		Wolfram Alpha: online Computer Algebra System *
47. John Henry and the End of Algebra	Lyrics to the folk song John Henry
48. Culture Jamming
49. The Future of the Obsolete	Marc Antony's speech from Shakespeare's Julius Caesar