Wallis's table of characteristic ratiosMove the yellow square to see the table entry. John Wallis, in Arithmetica Infinitorum (1656), presented this table. The column number is p, and the row number is q. The entry in the table is the ratio of the area under the curve The values of these areas were known for positive integer values of p and q. The value was also known for p=q=1/2, where the region is a quarter circle, with area This was a critical moment in mathematics: Isaac Newton read Wallis's book as a young man, and generalized the table to invent the binomial series. Newton was also the first to use fractional exponents. Note that the integer values are Pascal's triangle; the p,q entry is C(p+q,p). For details, see Wallis. Susan Addington, Created with GeoGebra |
| Mathematical Intentions |
Measuring the World |
Contact us |
Last updated January 28, 2018
Copyright 2009 David Dennis and Susan Addington. All rights reserved.

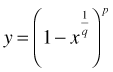 to the area of the circumscribed unit square; this is called the characteristic ratio of the function. We would now describe this an integral.
to the area of the circumscribed unit square; this is called the characteristic ratio of the function. We would now describe this an integral.